At its core, mathematics is all about decoding and understanding the rules and patterns that you can find everywhere you look. It’s no surprise that math is known as the ‘language of the universe.’ From the alignment of distant galaxies to the trends in the stock market, math can be used to predict, analyze, and interpret data from a variety of fields.
Nature has the potential to generate significantly more diversified things from the most basic of elements. Each of these inventions has a distinct essence, and each phenomenon revolves around a distinct concept. Nature must organize simple matter more strictly while making these different objects. This stricter way, in essence, is the embodiment of mathematics. Thus, mathematics is a key, a rule, and a secret behind diverse and beautiful creations. Origami, the ancient art of paper folding, is a lucid expression of this fact.
On the surface, it appears to be nothing more than a creative art form used to make small and fairly insignificant paper structures. However, origami serves a far greater purpose, and beneath the folds lie a plethora of equations and mathematical concepts that continue to redefine the craft.
Haga’s theorems are just one of the many mathematical principles that influence the world of origami.
Let ABCD be a square piece of paper of side length 1, and P be a point on AB. The theorem makes a generalization for any point P chosen.
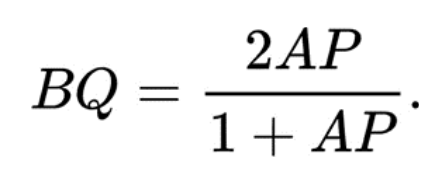
At first glance, this may seem rather insignificant, but this theorem cuts short the number of steps to divide a square’s side while also maintaining high levels of accuracy. For instance, you can obtain extremely obscure fractions in less than three steps.
With Haga’s Theorem, we can fold origami into odd parts like thirds and fifths, which would have otherwise been difficult to do without the theorem. This is rather groundbreaking in itself, given the widespread applications of origami.
Origami artists use Haga's theorems to fold lifelike animal models. For example, when designing a paper swan, the theorem helps determine where to place the folds to achieve the correct proportions for the swan's neck and wings. This precision ensures that the final creation closely resembles the actual swan.
Real-life applications
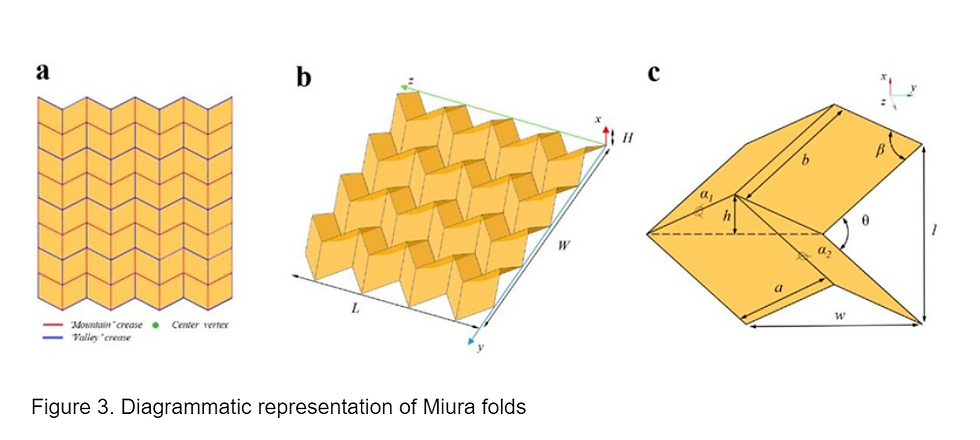
The Miura fold is a unique folding pattern that can be used to create a flat sheet of paper that can be unfolded into a three-dimensional shape. If you think about it, that’s what origami is all about: it is a way of transforming a flat sheet of paper into another shape with relatively little processing. The Miura fold employs a mathematical concept called a tessellation. A tessellation is a pattern of shapes that fills a surface without gaps or overlaps. In other words, it ‘tiles the plane.’ In the case of Miura folds, the tessellation is that of parallelograms.
Engineers use math to determine the stability of paper when folded in this way. Why would engineers be concerned, you ask? Well, Miura folds play an integral part in designing deployable structures, like solar panels for space exploration. Mathematicians use geometric calculations to create fold patterns that maximize the surface area of the panels that are exposed to space, which can optimize energy collection. Furthermore, folding the solar panels in this manner decreases the amount of space they take up, allowing them to be easily fitted within a rocket's payload bay.
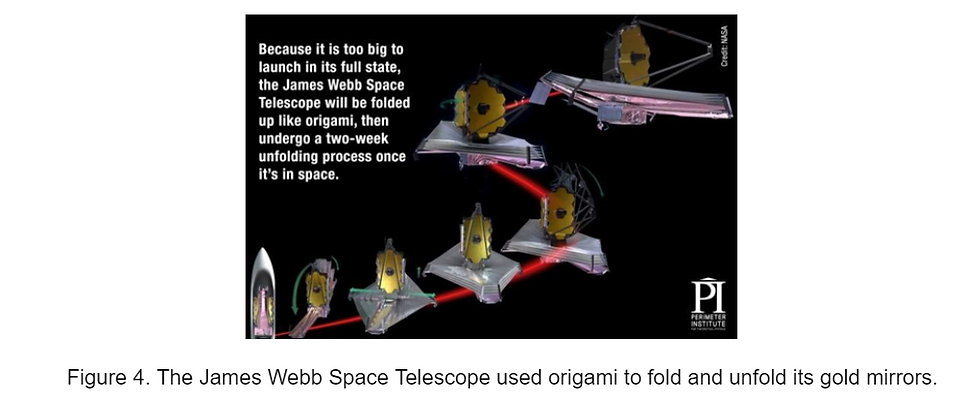
Origami’s reach extends even further. From medicine to robotics to even stopping bullets, origami is redefining the world of engineering. But one thing remains clear: all of it would not have been possible without mathematics.
The math of origami is indeed a complex and ever-evolving field. We can expect many more groundbreaking developments owing to origami as mathematicians and artists continue to explore the possibilities of this ancient art form.
By Siddharth Kannan, AS A
