I am sure we all have played or at least heard of the game called Super Mario before. It’s where an Italian plumber, with an iconic moustache and a red cap with a bold “ M”, jumps around the world, collecting coins and defeating monsters coming from sewers.
The most important component of the game is to jump to avoid treacherous holes and collect the coins scattered across the world. But did you know, when Mario jumps or in fact anyone jumps or throws anything into the air on earth in its uniform gravitational force, the path the person or object follows is the shape of a parabola and hence can be described via a quadratic function.
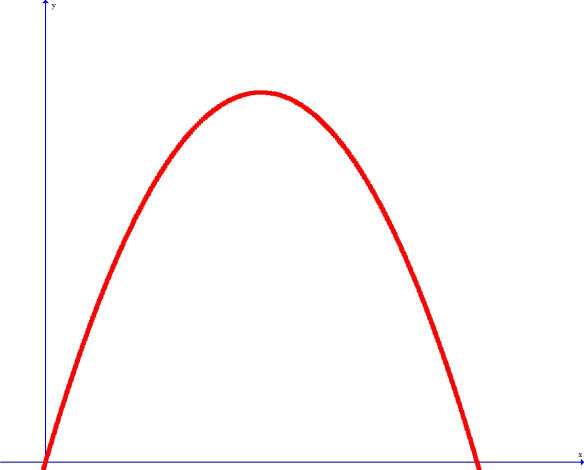
So keeping these things in mind, John Rowe, a teacher, made this game called Super Mario quadratics on a free online graphing tool called Desmos. This game is pretty identical to the real Super Mario game but instead of a joystick the players would have to construct and write various quadratics to collect coins and stars in a series of levels.
In the earlier rounds a pre-made quadratic is given and that has to be edited to help Mario reach his goal but as you progress further it gets more complex and in the end, the players have to form a quadratic function from scratch to win the game and help Mario save Princess Peach.
Now the game may seem very difficult. But it isn’t if you understand quadratic functions and what kind of parabolas they form.
A few simple rules of parabolas-
If you want to move the vertex of the parabola along the y-axis you would change the number you add or subtract from the values being squared (So in y = x2 +1 the vertex of the parabola would be at the y coordinate of 1)
If you want to move the vertex of the parabola along the x-axis you would change the number being added or subtracted from the x before it’s squared (So in y = (x+1)2 the vertex of the parabola would be at the x coordinate of -1)
If you want to make the parabola thinner you would increase the number that x is being multiplied by. If the number is negative then the parabola would turn inverse.
Let’s start off easy by looking at level 1
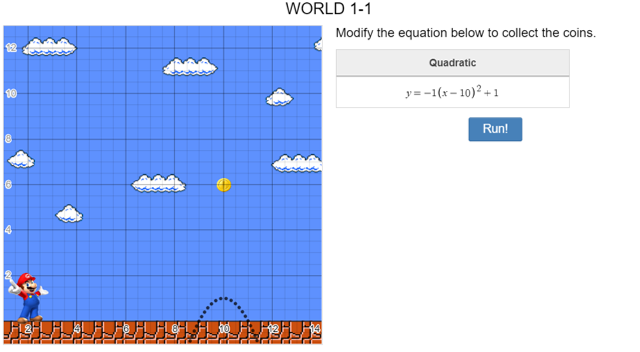
The parabola must be in a position where Mario can jump over the coin. So as we know if we increased the number being added after x is squared then the jump would get bigger in the y-axis. The coin is at the (10, 6) so if we increased the +1 to be a +6 then Mario would be succe
ssful in getting the coin as the parabola passes through the 6.
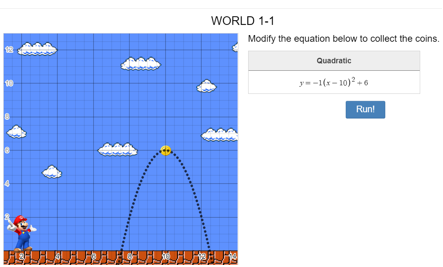
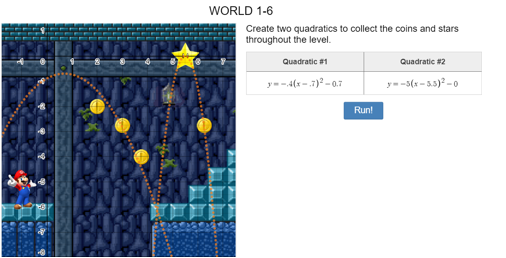
Now let’s get into a more interesting one level 6
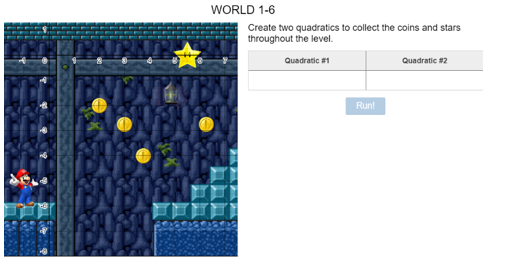
Here you need to create 2 different quadratics to complete the level.
The 1st quadratic needs to get Mario to the 3 coins in the air and he needs to land safely onto the platform. This can be done by subtracting 0.4 in the beginning making the parabola of perfect thickness and it also makes sure Mario gets from 1 platform to the other safely. Then subtracting 0.7 from x before squaring it would mean that the vertex would be at 0.7 on the x coordinate which gives the perfect trajectory for Mario to collect all the coins. After squaring, the values are subtracted by 0.7 to have the vertex high enough to reach all the coins. The quadratic would be: y = -0.4(x-0.7)^2-0.7
The 2nd quadratic needs to be quite thin so we would multiply x by a small number (-3). The star is at (5.5,0) so before squaring x it would be subtracted by 5.5 so the vertex of the parabola is at 5.5 on the x-axis.
The quadratic would be: y = -3(x-5.5)^2-0
There’s many more levels on the website that you can try out and see if you remember what you learned after reading this. I just showcased one way of solving these levels but you can write many more quadratics for just one level, so have fun with parabolas and help Mario save Princess Peach!!
Bibliography:
The game super Mario quadratics and all the images from the games- https://teacher.desmos.com/activitybuilder/custom/5c7614041509d870d4838bfd
First Mario image from- https://mario.nintendo.com/
Image of parabola -https://richbeveridge.wordpress.com/2009/10/23/area-under-a-parabola/
Desmos - https://teacher.desmos.com/
~BY DIVYANSHU PARIKH
Comentarios